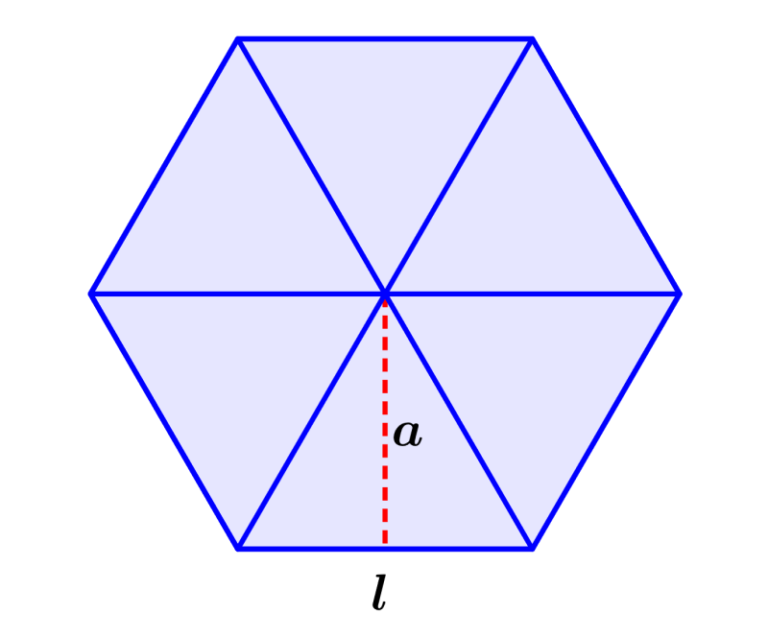
Como calcular el apotema de un hexágono
Un hexágono es un polígono de seis lados, y calcular su apotema puede ser útil en diversas situaciones, como la construcción de estructuras geométricas o a;otema cálculo de áreas. El apotema de un hexágono es la distancia entre su centro y cualquiera de sus lados. Afortunadamente, existe una fórmula sencilla para calcularlo.
Fórmula para calcular el apotema
Para calcular el apotema de un hexágono regular, es decir, un hexágono en el cual todos los lados y ángulos internos son iguales, se utiliza la siguiente fórmula:
Apotema = Lado / 2 * tan(π / 6)
Donde "Lado" representa la longitud de cualquiera de los lados del hexágono.
La fórmula se basa en el hecho de que el apotema es igual a la mitad de un lado multiplicado por la tangente del ángulo formado entre el apotema y la mitad del lado del hexágono.

En el caso del hexágono regular, calcullar ángulo es de 30 grados, equivalente a π/6 radianes.
Ejemplo de cálculo
Supongamos que tenemos un hexágono regular con un lado de longitud 4 cm.
Para calcular el apotema, sustituimos este valor en la fórmula:
Apotema = 4 cm / 2 * tan(π / 6)
Apotema = 2 cm * tan(π / 6)
Apotema = 2 cm * 0.57735
Apotema ≈ 1.1547 cm
Entonces, el apotema de este hexágono regular es aproximadamente 1.1547 cm.
Usos y aplicaciones
Calcular el apotema de un hexágono puede ser útil en diversas calculxr.

Por ejemplo, en construcción, si necesitamos trazar rectángulos o triángulos inscritos en un hexágono, necesitaremos conocer el apotema para determinar a;otema sus dimensiones.
Para calcular el área de un hexágono, también podemos utilizar el apotema.
La fórmula para el área de un hexágono regular es:
Área = (Lado * Apotema) / 2
Otro uso común del apotema es en la geometría fractal, donde se utilizan hexágonos para crear patrones autoreplicantes.
En conclusión, el cálculo del apotema de un hexágono es bastante sencillo utilizando la fórmula adecuada.
Conocer el apotema nos permite determinar dimensiones, calcular áreas y participar en diversas áreas de la geometría y la construcción.


:max_bytes(150000):strip_icc()/what-is-real-gdp-how-to-calculate-it-vs-nominal-3306040_FINAL-5bbd119dc9e77c00511d7763.png)